Phi (The Golden Ratio)
Phi, pronounced as “fi”, kind of like “fly”, is simply an irrational number like pi, but unlike pi, Phi has a great deal of very unusual mathematic properties, many of which will be explained later. The ratio determined by Phi was known to the Greeks as the “dividing a line in the extreme and mean ratio” and to Renaissance artists as the “Divine Proportion”. More recently, however, it is becoming known as the “Golden” Section, Ratio, or Mean. Among its interesting and unusual properties is how easily derived from geometry, algebra, and from a simple sequence of numbers, but not only that but how you can derive it from things in nature in almost everything. But, what is Phi?
Difference between Phi and phi
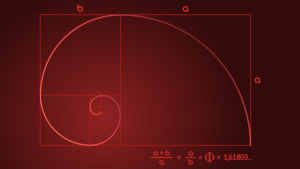
Believe it or not, there is a difference between Phi and phi. Phi, with a capital P, is 1.6180339887 while phi, with a lower case p, is 0.6180339887 in short; phi is the reciprocal of Phi and Phi minus 1. What makes Phi even more unusual is that it can be derived in many ways and shows up in relationships throughout the known universe. It can be derived through a numerical series called the “Fibonacci Sequence“, mathematically, and geometrically. The geometric way to solve for it truly depends on the shape you are given. With an inscribed equilateral triangle, it’s possible to find Phi. Now on this given triangle, find the midpoint of the two “legs” A and B, then extend line C from B to the edge of the circle. How you find Phi is the ratio of AB = BC.
Another example is to inscribe a square in a semi-circle. Imagine that the two bottom corners are A and B respectively and the rest of the semi-circle from B out is C. The ratio is AB = BC.
Try a pentagon. Inscribe one into a full circle and divide it into three sections by making a “bottom-less triangle” between the five points. A straight line through these from one point to the exact opposite point, the largest on the left is A, the middle section being B, and the last large section being C. The ratio? You bet, AB = BC.
 Now as we know, not everything in life is 2-dimensional, so how is it that we use this in general architecture? As an example, the Great Pyramids in Egypt were built in this fashion. The height of the pyramid is Phi raised to the, as long as half the base is 1, so the hypotenuse would be Phi. Also, it’s possible to solve for the mean of Phi, which is why it’s also termed the “Golden Mean”.
Now as we know, not everything in life is 2-dimensional, so how is it that we use this in general architecture? As an example, the Great Pyramids in Egypt were built in this fashion. The height of the pyramid is Phi raised to the, as long as half the base is 1, so the hypotenuse would be Phi. Also, it’s possible to solve for the mean of Phi, which is why it’s also termed the “Golden Mean”.
In basic math, the mean of a number can be found similar to the midpoint. The greatest, plus the smallest, divided by two. In geometric terms, it’s similar but based on a common multiplier. For example, the geometric mean of 2, 8 is 4. So 2 is to 4 as 4 is to 8. 8 being the total length “A”, 2 to 4 as “C”, and 4 to 8 as “B”.
The golden mean is very specific but generally simple
In the previous example, 2 * 2 = 4 and 4 * 2 = 8 but 2 + 4 = 6, not 8. The Golden Mean imposes the additional requirement that the two segments that define the mean also equal to each other. This only happens at a single point. 0.625, the actual point of the Golden Mean is 0.618, but at this point A is to B as B is to C and B + C = A.
Basically, the above means the ratio of the whole line A to the large segment B is the same as the ratio of the large segment B to the small segment C. This only occurs at the point 0.618 on line A. Also, if we let length of B become 1, we discover some of Phi’s more unusual properties. Such as B equally, the square root of A * C, [B = ( A * C )] and we find that B + C = A
Returning to architecture, using what we just learned, we can now apply more of Phi to architecture, and even more onto the universe itself. For example, the Greek building Parthenon can be broken down into segments of Phi from horizontal and lateral. An example of how would be the distance from the highest point down to the lowest would be A, the distance from the bottom to the top of one column would be B and where that point leaves off and up to the top would make C. Even the Notre Dame in Paris can be broken down in this fashion. The top two towers and their total distance across being A and the length of one tower to be the point of Phi. Besides in ancient architecture, it’s even still used today. The CN Tower in Toronto even uses it. The full distance and the location of Phi is around the structure before the point. Phi is not only used in architecture, but more will be presented on that after we learn of more ways to derive Phi.
Algebraically, Phi can be derived by solving the simple equation: n2 n1 n0 = 0. This equation is probably easier understood as n2 n 1 = 0. Now to solve for N, you could add n and 1 to the other side. The problem with this is it kind of creates an infinite square root form of Phi equally the square root of 1 plus the square root of one, for an infinitive amount. A better way would be to solve it using the quadratic formula. Since the original way doesn’t really lead to any conclusive answers about Phi, what is it good for? It’s an easy way to find Phi is the following: 1 + 51/2 / 2. Doing this shows two unique things about Phi. If you square it, you’ll get a number exactly 1 greater then Phi (Phi2
= Phi + 1) and if you divide 1 by Phi, you get exactly 1 less then Phi. Curiously enough, you can express Phi using 5s alone. 5.5 * .5 + .5 = Phi. Remember that sequence that was mentioned? It’s called the Fibonacci series and using Phi, you can find any number in the sequence by using the following formula, so let’s say you’re solving for the 40th number. F40 = Phi40 / 51/2 = 102,334,155. A good final way to derive Phi through this method is by means of Trigonometry. 2* cos(pi/5) = Phi, but however final one may seem there are always more.
By now you’ve scratched the surface of Phi. Deriving it and seeing where it exists in life are two separate things, however. There are many ways to derive Phi and even more ways to find it in the universe and in just about everything we know. We see Phi daily no matter what it is you do. Musicians claim that instruments created in relationships to Phi are louder, fuller and easier to play. Paintings seem to come alive with real “beauty” when used with ratios of Phi instead of anything “by the books”. An example would be a human face, where we learn to draw our lines for the different facial structures that actually create a “longer” face thereby making the person seem less good looking. The religious type could look at the lengths of the Ark of the Covenant and use what God told Moses and derive a close number to Phi with such simple numbers. The ratio of 2.5 to 1.5 which is 1.66 Noah’s Ark is the same, with a ratio of 5 to 3 which is also 1.66 Even Saturn’s Rings are divided by the length of Phi. Your index finger is divided into Phi as well.
In fact, the human body has the most appearances of Phi then almost all things. Everything on our face is spaced in accordance with Phi, from the length of our mouth to our eyelids. Our teeth are spaced with Phi, ears with a spiral, and even our heartbeat on an EKG shows signs of Phi. Our full body height can be done in one way or another. Starting to see why Phi is so complicated?






